Calculer les intérêts sur le marché monétaire

Les formules précomptées et les formules postcomptées.

Sur le marché monétaire, la formule sera celle des intérêts simples puisque les intérêts ne sont pas capitalisés. De plus, la période sera inférieure à un an (pas d’exposant donc). On l’appelle la Formule Générale :

Valeur finale = valeur initiale x (1 + taux x nombre de jour/360)
Taux = ((Valeur finale/valeur initiale -1) x (360/nombre de jours)) x 100
Valeur initiale = (valeur finale/(1+taux x nombre de jours/360)

Pour des intérêts précomptés, la valeur nominale du titre est la valeur remboursée à la échéance, c’est à dire la valeur finale. Donc lorsque l’investisseur achète le titre, il le paiera à un montant inférieur à la valeur nominale. La valeur d’achat est donc la valeur initiale :
Valeur initiale = Valeur finale / (1 + taux x nombre de jours/360)

Exemple de calcul :

1 000 000€ sont placés le 10/03 sur 30 jours au taux de 3.2%. Quelle est la valeur finale ?
Vf = 1 000 000 x (1 + 3.2% x 30/360)
Vf = 1 002 666.67 €

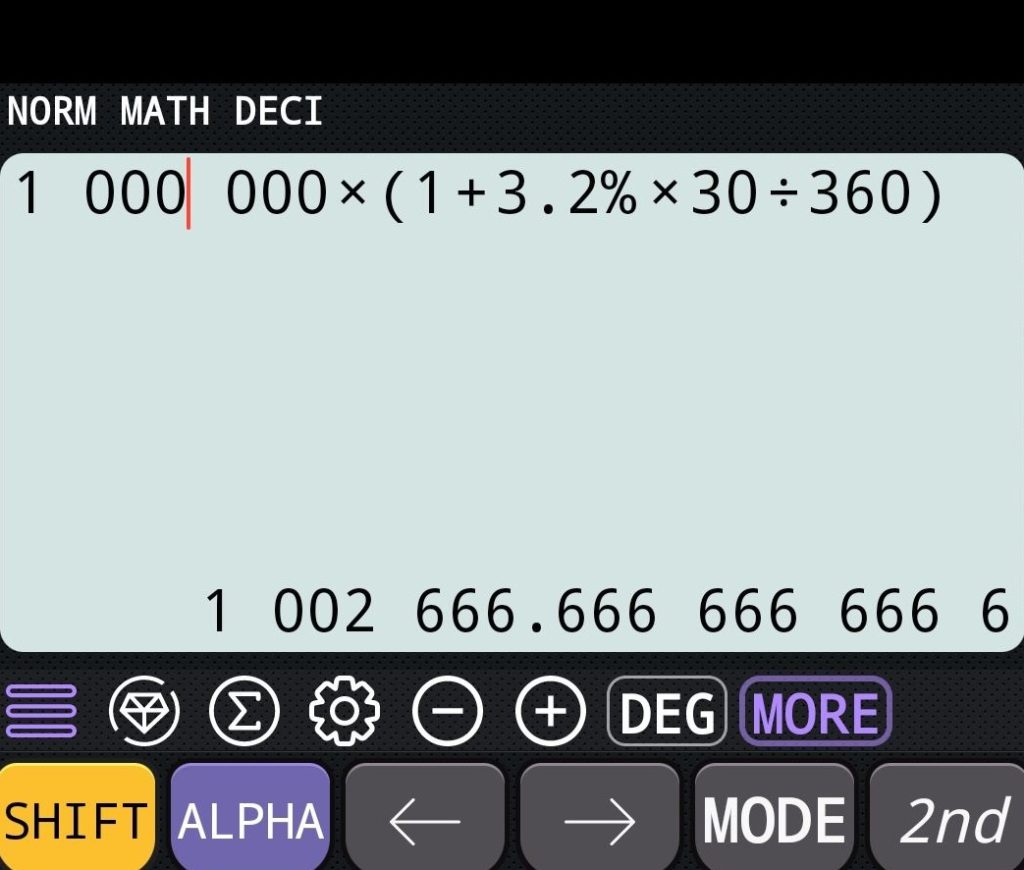
Autre exemple avec une fourchette à 3 mois.
Justement, la fourchette, qu’est-ce que c’est ?
Sur un marché dirigé par les prix, pour chaque titre coté, plusieurs « teneurs de marché » (market makers) sont en concurrence. Chaque teneur de marché énonce un double prix :
– un prix auquel il est immédiatement prêt à acheter (le « bid« , ou prix offert par le client)
– un prix supérieur auquel il est immédiatement prêt à vendre (« ask« , ou prix demandé)
Donc un acheteur va acheter au plus haut de la fourchette, un vendeur va vendre au plus bas de la fourchette (c’est logique, s’il achète au plus bas de la fourchette, il place ensuite immédiatement au plus haut et fait une plus-value simplement en restant assis devant son ordinateur..).
Reprenons l’exemple : la fourchette du 3 mois est cotée 3.15% – 3.20%. Je veux placer 100 millions d’euros sur 3 mois. Quelle valeur vais-je obtenir à l’issue ?
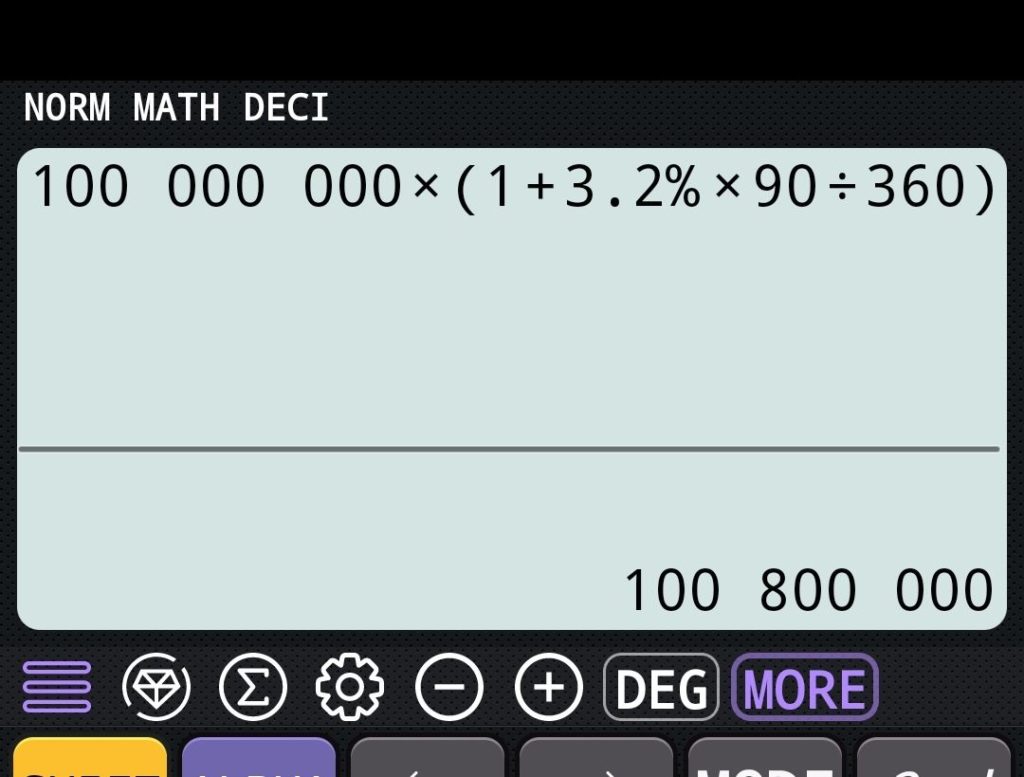
Vf = 100 000 000 x (1 + 3.2% x 90/360)
Vf = 100 800 000€

Si mon emprunteur me rembourse 102 500€, que j’ai placé il y a un mois au taux de 3.1%. Combien ai-je placé ?
Vi = 102 500 / (1 + 3.1% x 30/360)
Vi = 102 235.89 €

Un investisseur place 100 000€ sur 2 mois, avec une fourchette 3.30%-3.32%, puis place le capital et les intérêts sur 4 mois à une fourchette 3.42%-3.45%. Quel sera le taux réel sur 6 mois ?
On calcule le premier placement, puis le deuxième, et on applique la formule de calcul du taux.
100 000 x (1 + 3.30% x 60/360) = 100 550 €
puis
100 550 x (1 + 3.42% x 120/360) = 101 696.27 €
Et enfin
Taux = ((1 696.27/100000)x (360/180))x100 = 3.3925%

Le 10/03, un trésorier achète un Certificat de Dépôt négociable à échéance le 10/06 au taux de 3.36% pour un montant de 3 000 000€. Le 10/04, il décide de vendre son CDN, le taux à 2 mois est à 3.25%. Combien va-t-il toucher ? Quel est le gain engrangé en montant et en pourcentage ? Quel est le taux d’intérêt obtenu réellement ?
1er calcul : 3 000 000 x (1 + 3.36% x 90/360) = 3 025 200 €. Il sera remboursé in fine 3 025 200 €. Il va vendre son CDN en se basant sur ce prix, dans la mesure où l’acheteur place à 3.25% sur 2 mois. Il faut donc retrouver la valeur initiale sachant que la valeur finale est à l’issue de 3 mois. Il faut alors retirer 2 mois avec un taux à 3.25% –>
3 025 200 / (1 + 3.25% x 60/360) = 3 008 901.78 €
La valeur initiale du contrat à l’issue de 30 jours sera donc de 3 008 901.78€, ce qui signifie que le trésorier le vendra ce prix là. Quel gain peut-il escompter ? Et bien les 3 008 901.78€ vendu le 10/04 moins les 3 000 000€ placés au départ, soit 8 901.78€. En pourcentage, on applique la formule du taux : ((8 901.78/3 000 000)x(360/30)) x 100 = 3.5611 %.
Pourquoi le taux est supérieur au taux de départ ? Parce que le trésorier revend un gain sur un taux à 3 mois à un acheteur qui place sur un taux à 2 mois, inférieur. Mais celui qui rachète le CDN sur 2 mois obtiendra la même valeur finale que celle prévue à 3 mois.

Plus difficile, avec les Bons du Trésor à Taux fixe, dont la valeur nominale est la valeur finale.
Le 3/01, un trésorier achète un Bon du Trésor à taux fixe du 10/03 au montant de 5 000 000€, à un taux de 3.20%. La durée de placement est de 67 jours. Quel montant devra-t-il payer ? -> il faut retrouver la valeur initiale puisque les BTF sont à intérêts précomptés :
Vi = 5 000 000 / (1 + 3.20% x 67/360)
Vi = 4 970 398.51 € –> le trésorier devra payer cette somme pour obtenir ce BTF.
Le 02/02, il le revend à un taux de 3.3%. Réalise-t-il un gain ou une perte ? en % et en montant ?
La valeur nominale du BTF ne change pas, elle reste de 5 000 000€. Il faut là aussi retrouver la valeur initiale pour une valeur finale à 5 millions pour un taux de 3.30% sur une durée de 36 jours (du 2 février au 10 mars) :
Vi = 5 000 000 /(1 + 3.3% x 36/360)
Vi = 4 983 554.27 € –> Le trésorier revendra le BTF au prix de 4 983 554.27 €.
Pour calculer s’il réalise un gain ou une perte, il faut chercher la différence entre prix revendu et prix acheté : 4 983 554.27 – 4 970 398.51 = 13 155.76€ de gain. Pour l’établir en pourcentage, on applique la formule (partie/ensemble) x100 –> 13 155.76 / 4 983 554.27 x 100 = 0.26% ou bien ((Vf/Vi)-1)x100. Le gain est de 0.264%.
Le calcul du taux d’intérêt réel reprend la formule classique : (4 983 554.27/4 970 398.51 – 1) x (360/31) x 100 = 3.0737 %

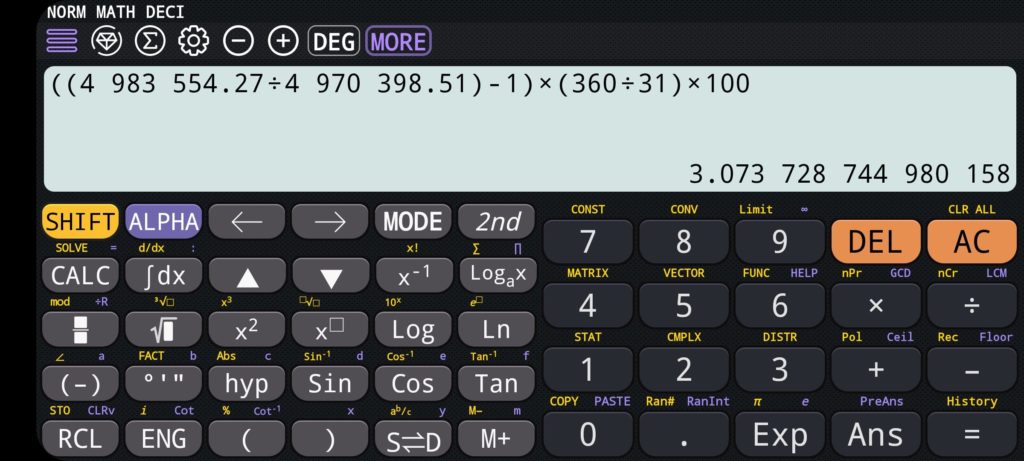
Exercice de calcul des durée moyenne pondérée et des taux moyens pondérés : La moyenne pondérée est la moyenne d’un certain nombre de valeurs affectées de coefficients. On considère les données M et les poids Alpha correspondants pour effectuer la formule suivante :

Les clients d’une banque ont effectués les dépôts suivants :
– DAT du client A : 100 000€ du 10 mars au 10 juin au taux de 2.5%
– DAT du client B : 150 000€ du 5 janvier au 10 décembre au taux de 2.80%
– DAT du client C : 500 000€ du 3 février au 10 aout au taux de 2.75%
Sachant que nous sommes le 10 avril, quelle est la durée restante à couvrir des DAT ?
Client A : 60 jours, client B : 240 jours, client C : 120 jours

Quelle est la durée moyenne des placements pondérée par les montants ?
On reprend la formule avec les données ici qui sont les durée, les poids pondérant sont les valeurs des placements, soit :
((100 000 x 60) + (150 000 x 240) + (500 000 x 120)) / (100 000 + 150 000 + 500 000) = 136 jours.

Quel est le taux moyen pondéré par les montants ?
Même formule, les données étant les taux, les valeurs étant le poids pondérant.
(100 000 x 2.5% + 150 000 x 2.80% + 500 000 x 2.75%) / (100 000 + 150 000 + 500 000) = 2.73%

Le client D a placé 650 000€ sur 6 mois à 3.4% et conservé 100 000€ en trésorerie placés au jour le jour au taux de 3.05%. Calculons la durée moyenne pondérée par les montants et le taux moyen pondéré par les montants.
((650 000 x 180 + 100 000 x 1) / (650 000 + 100 000) = 156,13 jours
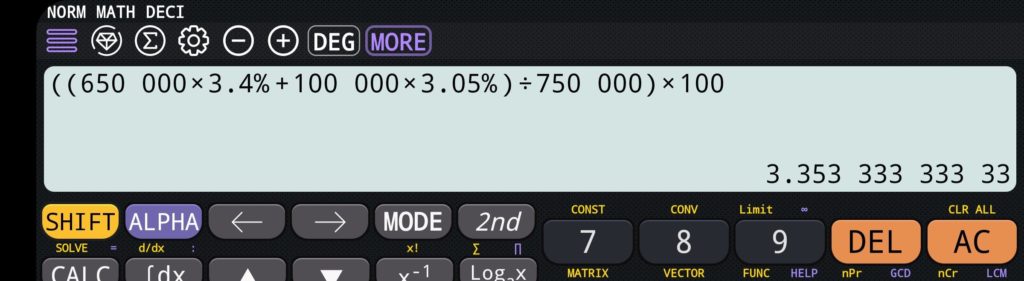
((650 000 x 3.4% + 100 000 x 3.05%) / (650 000 + 100 000) = 3.353%