
–> Les formules pour une échéance inférieure à un an avec intérêt annuel non capitalisé : base généralement admise de 360 jours pour une année
S’applique pour les opérations sur le marché monétaire, Bon du Trésor, CDN, inférieur à 1 an
Valeur future (VF) = valeur initial (Vi) x (1 + taux (annuel) x nombre jours / 360)
Valeur initiale (Vi) = valeur future (Vf) / (1 + taux (annuel) x nombre jours / 360)
Taux annuel= ((Valeur Future (Vf) / Valeur intiale (Vi))-1) x 360 / nombre de jours
–> Les formules pour une échéance supérieure à un an avec intérêts annuel capitalisés : base généralement admise de 365 jours pour une année

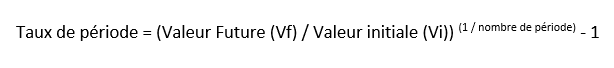
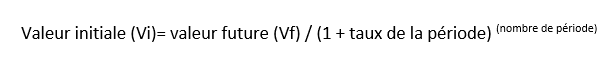
Attention, le taux de la période doit correspondre à la période (par exemple si vous avez un taux annuel et une période mensuelle, alors le taux de la période = taux annuel/12
Taux d’intérêt si le versement était fait tous les ans.

Exemple :
si votre argent rapporte un taux annuel de 6% capitalisé mensuellement, Cela veut dire que chaque mois, il faut calculer les intérêts sur :
Taux de la période (ou taux proportionnel) = 6%/12 = 0.5%


Taux actuariel :

Formules avec annuités constantes

Le change à terme
La règle : la devise que je vends, je l’emprunte, la devise que j’achète, je la prête
Acheter à terme une devise A par rapport à une devise B à une date T revient à :
– emprunter sur la période donnée la devise B
– la vendre au comptant contre la devise A
– placer la devise A au taux d’intérêt.
Vendre à terme une devise A par rapport à une devise B à une date T revient à :
– placer sur la période donnée la devise B
– après l’avoir achetée au comptant contre la devise A
– grâce à un emprunt de la devise A au taux d’intérêt.
Pour un cours A/B, tA est le taux de la devise qui mène, tB est le taux de la devise menée
La formule pour calculer le change à terme :
CT = change spot * (1+tB*nbre/360)/(1+tA*nbre/360)
Exemple :
LVMH va encaisser 1 200 000 USD dans 1 an de son client américain.
LVMH veut de suite fixer son revenu en EUR, et va vendre à terme à sa banque ces USD contre des EUR.
La banque va immédiatement emprunter des USD au taux de 1.4%/an.
La banque sait qu’elle devra rembourser ces USD 1.2 millions dans 1 an, il faut donc qu’elle emprunte la Valeur initiale pour pouvoir fournir la Valeur finale dans 1 an.
Formule : Vi = Vf/(1+tx*Nbre/jours) soit 1 200 000 / (1+0.014% * 360/360)
Vi = 1 200 000 / 1.014 = USD 1 183 432
Elle emprunte donc USD 1 183 432 (qu’elle devra rembourser dans 1 an), et elle les change immédiatement en EUR, au taux de EUR/USD 1.2813.
Soit 1 183 432 / 1.2813 (le USD étant moins cher, elle aura donc moins d’EUR qu’elle n’avait de USD) = EUR 923 618
Ensuite, elle place ces EUR au taux de 2.2% sur 1 an. Ce qui représente au bout d’1 an ?
Vf = Vi*(1+tx*nbre/jour), soit 923 618 * (1+2.2%*360/360)
Vf = 923 618 * 1.022 = EUR 943 938
Elle rembourse ensuite son premier emprunt en USD avec la somme que LVMH va lui verser dès que LVMH encaisse sa facture, qui sera donc en USD. Si la banque veut juste couvrir ses couts, quel serait alors le change à terme que la banque française va facturer à LVMH ?
Soit 1 200 000/943 938 = 1.2713
ou
CT = cours spot * (1+tx de devise B*nbre jours/360)/(1+tx de devise A*nbre jours/360)
Soit
1.2813*(1+1.4%*360/360)/(1+2.2%*360/360) =
1.2813 * (1.014/1.022)) = 1.2713
La banque va annoncer un taux de change EUR/USD de 1.2713 à LVMH, et lui annonce qu’elle versera à LVMH un montant de 943 938 € dans 1 an.
Si la banque facture 1% de frais pour les opérations effectuées, alors le montant final sera :
943 938 * 0.99 = 934 498 €
Quel sera le montant réel du taux de change du coup ?
Pour 1 200 000, on obtient 934 498, donc coeff. multiplicateur : 1 200 000/ 934 498 = 1.2841
Le taux réel appliqué à LVMH pour un change à terme EUR/USD est de 1.2841
C’est la banque qui supporte le risque de change, puisque l’opération à terme implique une opération au comptant.
Supposons que Smith&Wesson vend des GBP dans 3 mois, contre des USD.
Taux 3 mois GBP: 3.90% – 3.93%
Taux 3 mois USD : 1.09% – 1.10%
Spot GBP/USD : 1.6942 – 1.6945
Quel taux propose la banque ?
La banque emprunte immédiatement des GBP à 3.93% qu’elle devra rembourser dans 3 mois.
Elle les vend (au plus bas 1.6942) pour acheter des USD qu’elle prête au plus bas (1.09%)
Dans 3 mois, elle remboursera les USD avec la somme que lui donnera S&W
Soit un CT = 1.6942*(1+1.09*90/360)/(1+3.93%*90/360)
Soit CT = 1.6825
– Le coupon couru
Le coupon couru d’une obligation est la fraction d’intérêts annuel écoulé depuis le dernier versement des intérêts jusqu’à la date actuelle. Ainsi, le vendeur d’une obligation ne sera pas lésé car il touchera sa part d’intérêt sans devoir attendre la prochaine tombée du coupon. (ici, 4 days)
– Le prix déboursé : le prix déboursé sera égal au Nominal * prix de l’obligation + coupons courus
Avec coupons courus = Nominal*taux d’intérêts de l’obligation (coupon) * nombre de jours courus/365
Les exercices d’application :
1) Calculer le montant à rembourser d’un Dépôt A Terme de 150 000 euros sur 60 jours, taux 2,5%.
La formule : (VF) = (Vi) x (1 + taux (annuel) x nombre jours / 360)
Vf = 150 000 x (( 1 + 2.5 % x 60/360) = 150 625 €

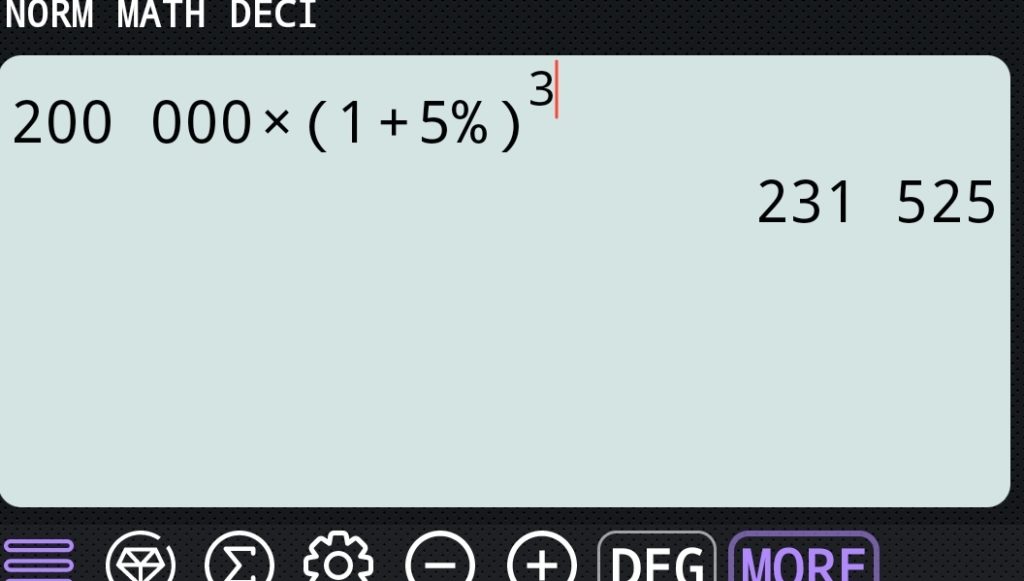
2) Calculer le montant à rembourser d’un emprunt de 200 000 euros sur 3 ans à un taux annuel de 5% (pas de remboursements intermédiaires).
La formule : Vf = Vi x (1 + taux)N
Vf = 200 000 x ( 1 + 5%)3 = 231 525 €
3) Calculer le montant emprunté d’un placement qui sera remboursé 393 702,4 euros dans 3 ans, taux 4%.
Il faut trouver la valeur initiale donc : valeur future / (1+taux)N
393 702,4 / (1+4%)3 = 350 000€

4) Si je place 500 000 euros et que dans 15 ans mon placement me rapporte 1 084 914,65 euros, quel est mon taux de placement ?
Il faut trouver le taux donc formule : Vf/Vi1/n – 1
(1 084 914.65 / 500 000)(1/15) -1 = 5.3%
5) Est-il plus intéressant d’emprunter 100 sur deux ans à un taux de 2.5% semi-annuel ou d’emprunter à un taux de 5% annuel ?
Emprunt 100 sur 2 ans à 2.5% semi-annuel :
100 * (1+2.5%)*(1+2.5%)*(1+2.5%)*(1+2.5%) = 100*(1+2.5%)4 =110.38
Taux actuariel = (110.38 / 100)1/2 – 1= 5.06%
Emprunt de 100 sur 2 ans à 5% = 100 * (1+5%)2 = 110.25
Il vaut mieux emprunter à 5% sur 2 ans : 110.25 < 110.38
6) On vous propose un emprunt de 100 000 euros sur 3 ans : 2.5% première année, puis 3.5% les deux années suivantes. Quel est le taux actuariel ?
100 000 * (1+2.5%) * (1+3.5%) * (1+3.5%) = 109 800.56 €
Taux actuariel = (109 800.56/100 000)1/3 – 1 = 3.17%
7) Vous épargnez 100 euros par an sur les trois prochaines années. Combien obtiendrez-vous si le taux est de 5% / an ? (1er versement en fin de la première année).
VF = 100 * (1+5%)2 + 100 * (1+5%) + 100 = 315.25
Ou en appliquant la formule des annuités constantes :
VF = 100*((1+5%)3 -1) / 5% = 315.25
8) Combien vous faudra-t-il placer dans une assurance vie qui vous rapporte 5%/an, pour pouvoir retirer 100 euros/an sur les trois prochaines années ? (1er flux fin d’année).
100 / (1+5%)3 + 100/(1+5%)2+100/(1+5%)=272.32
Ou en appliquant la formule des annuités constantes :
VA = 100 * (1-(1+5%)-3) / 5%=272.32
9) Vous avez besoin d’emprunter 100 000 euros pour l’achat d’un appartement. Votre banque vous propose un prêt immobilier à rembourser sur trente ans en 360 mensualités constantes au taux de 6% annuel. A combien se montent les mensualités ?
Formule des annuités : Vi x Taux / (1-(1 + taux)-n
Mensualité = 100 000 * 0.5% / (1-(1+0.5%)-360 = 599.55

Poster un Commentaire
Vous devez vous connecter pour publier un commentaire.